PyTorch 基本概念和用法

Posted on Edited on In

PyTorch 是基于 Python 的科学计算包，官网给它自己的定义是：

  1. A replacement for NumPy to use the power of GPUs
  2. A deep learning research platform that provides maximum flexibility and speed

可以看出，PyTorch 提供了一种类似 Numpy 的抽象方法来表征张量（或多维数组），它还能利用 GPU 来提升性能。

基础数据结构

PyTorch 的关键数据结构是张量 (Tensors)，即多维数组。其功能与 NumPy 的 ndarray 对象类似，不同的是它可以在GPU上使用。

  • 张量的基本操作可见于这里
  • 张量和Numpy的互相转换： 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# from tensor to ndarray
>>> a = torch.ones(3)
>>> b = a.numpy()
>>> a.add_(1)
>>> print(b)
[2. 2. 2.]

# from ndarray to tensor
>>> a = numpy.ones(4)
>>> b = torch.from_numpy(a)
>>> numpy.add(a, 1, out=a)
array([2., 2., 2., 2.])
>>> print(b)
 2
 2
 2
 2
[torch.DoubleTensor of size 4]

值得注意的是，Torch Tensor 和 NumPy array 其实是共享内存位置的，因此改变一个另一个也会因此改变。

  • 张量使用GPU加速计算
1
2
3
4
5
6
7
8
9
10
11
12
# Tensors can be moved onto GPU using the .cuda method.
>>> x = torch.rand(3,4)
>>> y = torch.rand(3,4)
>>> if torch.cuda.is_available():
...     x = x.cuda()
...     y = y.cuda()
...     print(x+y)
... 
 0.8296  1.5523  0.8696  1.4905
 0.7956  0.5263  0.6687  1.7677
 1.0483  0.7037  0.8505  1.5983
[torch.cuda.FloatTensor of size 3x4 (GPU 0)]

自动微分库

自动微分库autograd是 PyTorch 用于所有神经网络计算的关键库，它提供了所有关于张量的微分操作。Autograd 是基于动态框架的，这意味着反向传播根据代码运行状态而改变，每次迭代过程中都可能不同。

autograd.Variable 是这个包中最重要的类。它：

  • 是张量的简单封装
  • 记录了所有历史操作
  • 将梯度保存在 .grad 中
  • 可以帮助建立计算图

每次结束计算后，使用.backward()可以自动计算出所有梯度值：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
>>> from torch.autograd import Variable
>>> x = torch.randn(3)
>>> x = Variable(x, requires_grad=True)
>>> y = x * 2
>>> while y.data.norm() < 1000:
...     y = y * 2
... 
>>> print(y)
Variable containing:
 908.8007
 549.7198
 507.9812
[torch.FloatTensor of size 3]

# through .data we can access raw tensor
>>> print(y.data)
 908.8007
 549.7198
 507.9812
[torch.FloatTensor of size 3]

# .grad_fn references a Function that has created the Variable 
# (except for Variables created by the user - their grad_fn is None).
>>> print(y.grad_fn)
<MulBackward0 object at 0x7ffa1ea95470>
>>> print(x.grad_fn)
None

# we can call .backward() on a Variable to compute the derivatives. 
# If Variable is a scalar (i.e. it holds a one element data), you don’t need to specify any arguments to backward(), however if it has more elements, you need to specify a gradient argument that is a tensor of matching shape.
>>> gradients = torch.FloatTensor([0.1, 1.0, 0.0001])
>>> y.backward(gradients)
>>> print(x.grad)
Variable containing:
  51.2000
 512.0000
   0.0512
[torch.FloatTensor of size 3]

神经网络

torch.nn包可以用来构建神经网络。一个nn.Module包含了layers和用于返回output的forward(input) 方法。

例如这个简单的前馈神经网络：

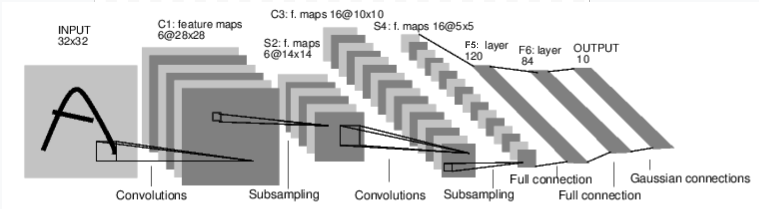
一般典型的神经网络训练步骤如下：

  1. 定义带学习参数 (learnable parameters or weights) 的神经网络；
  2. 输入数据集进行迭代计算；
  3. 使用神经网络处理输入；
  4. 计算损失；
  5. 将梯度返回到网络的参数中；
  6. 更新参数。

定义神经网络

定义一个神经网络只需要定义其：

  • 层结构 (Layers)
  • 前馈函数 (Forward function)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
"""
You just have to define the forward function, and the backward function 
(where gradients are computed) is automatically defined for you using autograd. 
You can use any of the Tensor operations in the forward function.
"""

import torch
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):
	# Define the basic layer structure 
   def __init__(self):
        super(Net, self).__init__()
        # 1 input image channel, 6 output channels, 5x5 square convolution
        # kernel
        self.conv1 = nn.Conv2d(1, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)
	
	# Define the forward function and automaticly generate backward function
   def forward(self, x):
        # Max pooling over a (2, 2) window
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # If the size is a square you can only specify a single number
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = x.view(-1, self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

    def num_flat_features(self, x):
        size = x.size()[1:]  # all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s
        return num_features


net = Net()
print(net)

# The learnable parameters of a model are returned by net.parameters()
params = list(net.parameters())
print(len(params))
print(params[0].size())  # conv1's .weight

# ---------------- Output Result: ----------------------
Net(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)
10
torch.Size([6, 1, 5, 5])

损失函数、反向传播与参数（权重）更新

nn中已经定义了许多损失函数，其中一个简单的是nn.MSELoss，用于计算均方误差。

最简单的权重更新规则是随机梯度下降（Stochastic Gradient Descent, SGD）：
weight = weight - learning_rate * gradient

同时，torch.optim为更新权重提供了优化算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import torch.optim as optim

input = Variable(torch.randn(1, 1, 32, 32)) # a dummy input, for example
target = Variable(torch.arange(1, 11))  # a dummy target, for example
target = target.view(1, -1)  # make it the same shape as output

# define the loss function
criterion = nn.MSELoss()

# create your optimizer
optimizer = optim.SGD(net.parameters(), lr=0.01)

# do the training loop:
for epoch in range(10):
	optimizer.zero_grad() # Zero-out previous gradients
	output = net(input)
	loss = criterion(output, target)
	loss.backward() # Compute new gradients
	optimizer.step() # Apply these gradients and do the update
	
# Updated parameters are available at net.parameters()

参考资料

[1] 从头开始了解PyTorch的简单实现